Unified District Model
December 2020
In order to score new plans, it is necessary to create a statistical model of the relationship between districts’ latent partisanship and candidates’ incumbency status with election outcomes. This enables us to estimate district-level vote shares for a new map and the corresponding partisan gerrymandering metrics. This page describes the details of our methodology and how we validate the results of this model.
Results for uncontested elections are imputed as described in The Impact of Partisan Gerrymandering on Political Parties and its appendix, by Nicholas Stephanopoulos and Christopher Warshaw.
Methodology
The vote share inputs for calculating the metrics come from a Bayesian hierarchical model of district-level election returns, run for all state legislatures and congressional delegations on the elections from 2012 through 2018. Formally, the model is:

where
- i indexes district level elections
- s indexes states, with s(i) denoting the state of district election i
- c indexes election cycles, with c(i) denoting the election cycle of district election i
- yi is the Democratic share of the two-party vote in district election i
- Xi is a matrix of covariate values for district election i
- β is a matrix of population-level intercept and slopes corresponding to covariates X
- βs(i) and βc(i) are matrices of coefficients for the state and election cycle, respectively, of district election i
- σy is the residual population-level error term
The model includes two covariates: 1) the two-party district-level Democratic presidential vote share, averaged across 2012 and 2016 and centered around its global mean; 2) the incumbency status in district election i, coded -1 for Republican, 0 for open, and 1 for Democratic. The model allows the slope for each–as well as the corresponding intercept– to vary across both states and election cycles. Chambers accounted for minimal variation in an ANOVA test, so state legislative and congressional results were modeled together as emerging from a common distribution.
When generating predictions, PlanScore assumes an average election year for the 2012- 2018 period (βc = 0), but otherwise draws from the posterior distribution of model param- eters for means and probabilities.
| Estimate | 95% Credible Interval | |
|---|---|---|
| POPULATION-LEVEL | ||
| Intercept (β0) | 0.50 | [0.45, 0.55] |
| Presidential vote (β1) | 0.79 | [0.58, 1.00] |
| Incumbency (β2) | 0.05 | [0.02, 0.08] |
| STATE-LEVEL | ||
| Standard Deviations | ||
| Intercept (σβ0s) | 0.02 | [0.02, 0.03] |
| Presidential vote (σβ1s) | 0.13 | [0.10, 0.16] |
| Incumbency (σβ2s) | 0.02 | [0.02, 0.03] |
| Correlations | ||
| Intercept - Pres. vote (ρσβ0sσβ1s) | −0.41 | [−0.62,−0.15] |
| Intercept - Incumbency (ρσβ0sσβ2s) | 0.11 | [−0.17, 0.39] |
| Pres. vote - Incumbency (ρσβ1sσβ2s) | −0.73 | [−0.85,−0.56] |
| CYCLE-LEVEL | ||
| Standard Deviations | ||
| Intercept (σβ0c) | 0.04 | [0.01, 0.14] |
| Presidential vote (σβ1c) | 0.18 | [0.07, 0.48] |
| Incumbency (σβ2c) | 0.02 | [0.01, 0.07] |
| Correlations | ||
| Intercept - Pres. vote (ρσβ0cσβ1c) | −0.13 | [−0.84, 0.70] |
| Intercept - Incumbency (ρσβ0cσβ2s) | −0.23 | [−0.89, 0.68] |
| Pres. vote - Incumbency (ρσβ1cσβ2c) | −0.46 | [−0.95, 0.54] |
| Note: Model estimated in brms for R. Model based on 4 MCMC chains run for 4000 iterations each with a 2000 iteration warm-up. All model parameters converged well with R < 1.01. | ||
Predictions
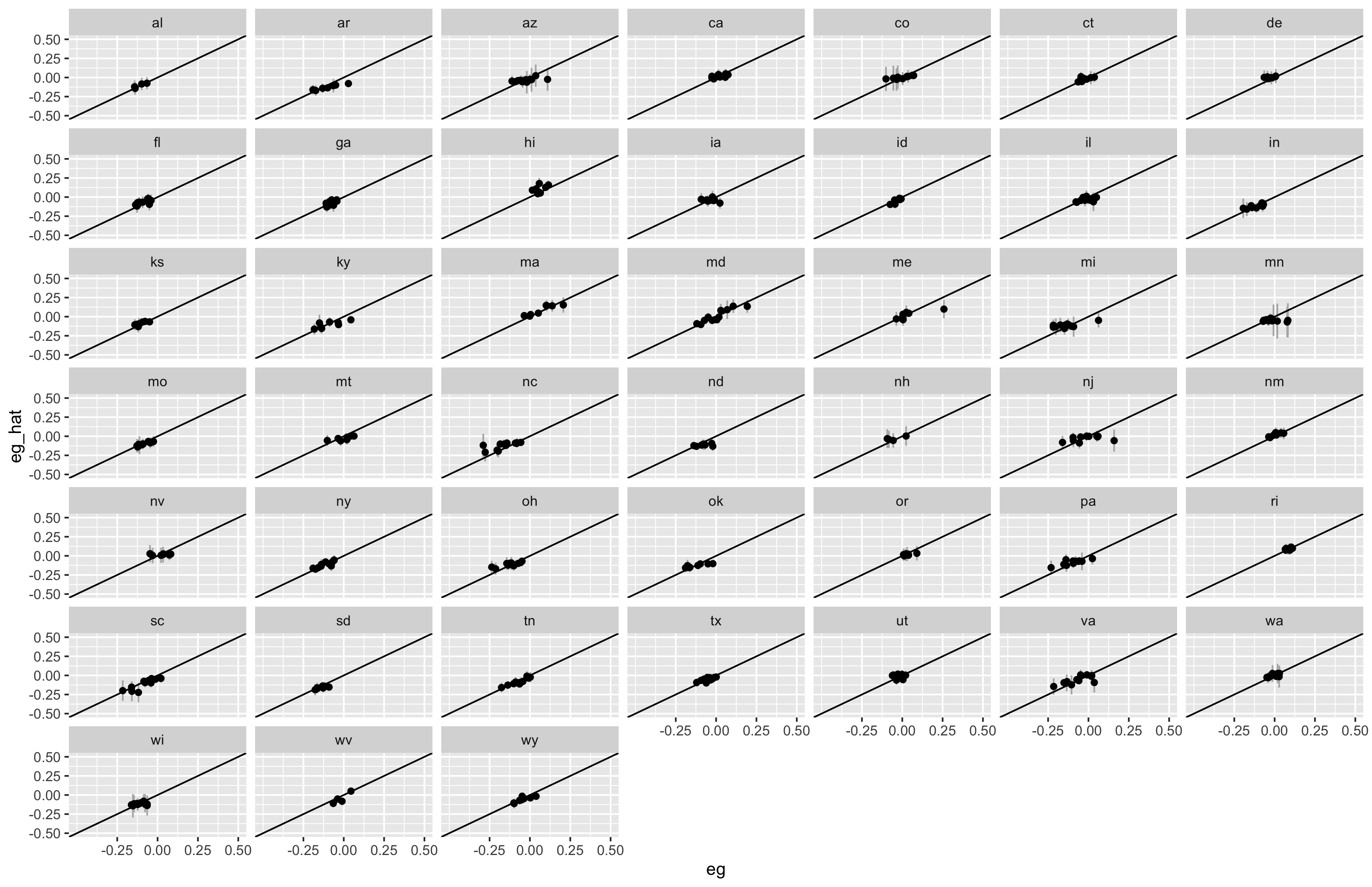
The charts below show comparisons between this model’s in-sample predictions and observed historical scores for plans with at least 7 districts. The results were broadly similar for cross-validated predictions with 10 percent of the sample set aside for testing. The predictions were also quite strong for 2020 in states where we were able to obtain election results for comparison.


Data Sources
Precinct-level presidential vote data used by this model is mostly sourced from the Voting and Election Science Team at University of Florida and Wichita State University.